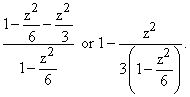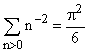|
There are functions that are not integrable in general but for which integrals
between certain specific endpoints can be evaluated. These are often integrals
that can be rewritten, either by adding a known integral, or by using symmetry,
or by some other trick, as an integral over a closed path in the complex plane.
Such integrals can be evaluated by use of the Residue Theorem, which states that
the integral of a function f(z) counterclockwise around a simple closed path C
is 2 i
times the sum of the residues of f within C. The residue of a function with an
isolated singularity is the coefficient of its minus first power at the singular
point. i
times the sum of the residues of f within C. The residue of a function with an
isolated singularity is the coefficient of its minus first power at the singular
point.
Thus for example, 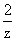 has residue 2 at z = 0.
has residue 2 at z = 0. 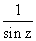 has
residue 1 at even multiples of has
residue 1 at even multiples of  ,
and residue -1 at the odd multiples of ,
and residue -1 at the odd multiples of  . .
We know that the function 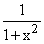 is the derivative of the arctangent, so we can actually integrate it over any
range. In particular since we have
is the derivative of the arctangent, so we can actually integrate it over any
range. In particular since we have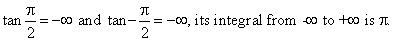
Here is another way to deduce this fact. We can use partial fractions to write
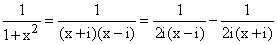
Thus this function has a singularity at i in the upper half plane and a singularity
at -i in the lower half plane, with residues 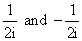 respectively. If we make a path C that goes up the real axis from -R to R then
around a semicircle in the upper half plane from R back to -R, for R > 1 this
will enclose the singularity at i.
respectively. If we make a path C that goes up the real axis from -R to R then
around a semicircle in the upper half plane from R back to -R, for R > 1 this
will enclose the singularity at i.
The value of the integral will therefore be 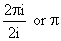 ,
by the residue theorem. The integrand will behave like ,
by the residue theorem. The integrand will behave like  on the large semicircle, and since the length of that semicircle is only
on the large semicircle, and since the length of that semicircle is only  R,
the integral around it will go to zero like 1/R does as R increases. This tells
us that the value of the integral from -R to R on the real line will go to R,
the integral around it will go to zero like 1/R does as R increases. This tells
us that the value of the integral from -R to R on the real line will go to  as R increases.
as R increases.
This gives us an integral we know. However the same technique applies to much
more complicated integrands and allows us to do lots of integrals again from -R
to R as R approaches infinity. We give two examples. One is the so called Fourier
transform of 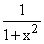 . .
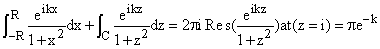
where C is the semicircle of radius R in the upper half plane, and again the
integral on C goes to zero as R increases.
Now we use this method to sum a series. The function cot x is singular at
x = 0 and is periodic with period  so it is singular at every multiple of
so it is singular at every multiple of  .
Its residue at each of these singularities is 1. Moreover, if you wander far off
the real line, it quickly approaches either i or -i, since it is .
Its residue at each of these singularities is 1. Moreover, if you wander far off
the real line, it quickly approaches either i or -i, since it is
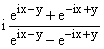
and the second terms in the numerator and denominator will dominate in the
upper half plane making the integrand approach -i and the first terms will dominate
in the lower half plane so that it approaches i as |y| increases there.
This implies that an integral of 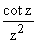 over a large circle of radius R (with R a half integral multiple of
over a large circle of radius R (with R a half integral multiple of  to avoid trouble near the real line) will go to zero as R goes to infinity just
as in the previous case. This further implies that the sum of the residues of
this function must go to zero inside this circle. But for each positive or negative
integer j the residue of this function at
to avoid trouble near the real line) will go to zero as R goes to infinity just
as in the previous case. This further implies that the sum of the residues of
this function must go to zero inside this circle. But for each positive or negative
integer j the residue of this function at 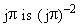 .
The residue of this integrand at z = 0 can be computed as half the second derivative
of z cot z at z = 0. (we factor out the singular term which is here z-3
and expand the rest of the integrand in a Taylor series to get z-1
coefficient. ) .
The residue of this integrand at z = 0 can be computed as half the second derivative
of z cot z at z = 0. (we factor out the singular term which is here z-3
and expand the rest of the integrand in a Taylor series to get z-1
coefficient. )
Since sin z goes as 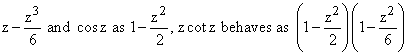 which can be written as
which can be written as 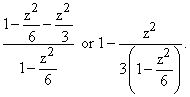
The residue of 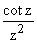 at z = 0 is therefore -1/3 and we obtain the conclusion:
at z = 0 is therefore -1/3 and we obtain the conclusion:
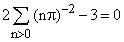
or
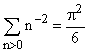
You can actually sum the first 128 (or 1024) terms of this sum on a spreadsheet
and extrapolate by comparing the sum up to different powers of 2. If you extrapolate
first forming S2(k) = S(2k)-S(2k-1), then S3(k) = (4S2(k)-S2(k-1))/3
then
S4(k) = (8S3(k)-S3(k-1))/7, etc. You can get this answer to enormous accuracy
numerically and verify this conclusion.
|

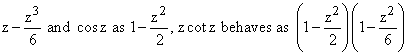 which can be written as
which can be written as