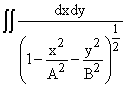| |
|||||
A flux integral is one of the general form:
Suppose now we have a parametric representation for S, which means we have
equations x = x(u, v), y = y(u, v) and z = z(u, v), which define our surface.
We can reduce this integral to a sequence of ordinary integrals over u and v by
expressing (W form the vectors
and similarly
Then the integrand, integrating over u and v, can be written as the absolute
value of the determinant of the matrix with columns given by the components of
W,
While this reduction straightforward, the steps necessary to perform it in
practice involve a sufficient amount of algebraic manipulation that I for one
almost always make at least one error in doing it, and so rarely get the same
answer twice. Fortunately there is a computationally simpler answer in the most
common case, in which u and v are actually two of your original variables, say
x and y.
which result is much easier to apply. We have assumed here that the sign should
be positive in the direction that is upward in the z direction, and it must be
reversed if that assumption is incorrect.
(when The answers given here give both the integrand and the area element. The only time you really have to worry about the area element is when you want to change variables and have to determine what the area element dxdy means in terms of other variables u and v. Here is an example: We want to compute the flux of the vector (x, y, z) outward through the surface defined by the equation
(This surface is called an ellipsoid). We will integrate over the portion of the surface for which z > 0 only and
double the result since the lower part of the surface gives the same flux.
over appropriate limits of integration. Those limits are the bounds (which we will discuss below) determined by the area in the xy plane that we are integrating over, and that is, the region in which the denominator in that integral is positive. |
||||||||||||||||||||||||||

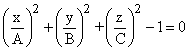
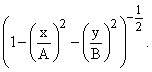 Our integral therefore becomes
Our integral therefore becomes