Course Description
This course introduces students to the fundamentals of nonlinear optimization theory and methods. Topics include unconstrained and constrained optimization, linear and quadratic programming, Lagrange and conic duality theory, interior-point algorithms and theory, Lagrangian relaxation, generalized programming, and …
This course introduces students to the fundamentals of nonlinear optimization theory and methods. Topics include unconstrained and constrained optimization, linear and quadratic programming, Lagrange and conic duality theory, interior-point algorithms and theory, Lagrangian relaxation, generalized programming, and semi-definite programming. Algorithmic methods used in the class include steepest descent, Newton’s method, conditional gradient and subgradient optimization, interior-point methods and penalty and barrier methods.
Course Info
Learning Resource Types
theaters
Lecture Videos
notes
Lecture Notes
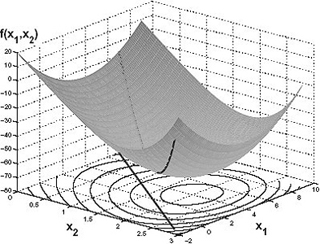
A convex function to be optimized. (Graph courtesy of Prof. Robert Freund.)








