Course Description
Functional analysis helps us study and solve both linear and nonlinear problems posed on a normed space that is no longer finite-dimensional, a situation that arises very naturally in many concrete problems. Topics include normed spaces, completeness, functionals, the Hahn-Banach Theorem, duality, operators; Lebesgue …
Functional analysis helps us study and solve both linear and nonlinear problems posed on a normed space that is no longer finite-dimensional, a situation that arises very naturally in many concrete problems. Topics include normed spaces, completeness, functionals, the Hahn-Banach Theorem, duality, operators; Lebesgue measure, measurable functions, integrability, completeness of Lᵖ spaces; Hilbert spaces; compact and self-adjoint operators; and the Spectral Theorem.
Course Info
Instructor
Departments
Learning Resource Types
assignment
Problem Sets
grading
Exams
notes
Lecture Notes
theaters
Lecture Videos
Editable Files
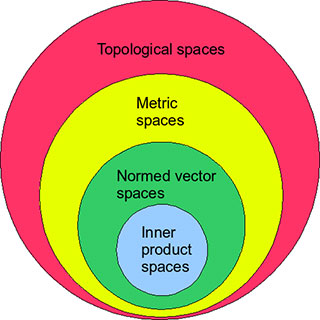
A hierarchy of mathematical spaces: The inner product induces a norm. The norm induces a metric. The metric induces a topology. (Image by Jhausauer,on Wikimedia Commons. Public domain.)








