Differential Analysis

Calendar

Lec #	TOPICS	KEY DATES
1	Space of Continuous Functions, Dual Space, Positivity
2	Outer Measures and Measures
3	Caratheodory’s Theorem
4	Measurable Functions and the Integral - Including Lebesgue’s Theorem of Dominated Convergence
5	Riesz Representation, Lp Spaces and Completeness, L2(X,μ) and Hilbert Space	Problem set 1 due
6	Riesz Representation for Hilbert Space Differentiability and Schwartz Space of Test Functions	Problem set 2 due
7	Properties of S(Rn) Tempered Distributions Differentiation and Differential Operators Fourier Transform
8	Bump Functions Characterization of δ Fourier Inversion Plancherel Formula	Problem set 3 due
9	Convolution and Density Fourier Transform on L2(Rn)
10	Sobolev Spaces and Sobolev Embedding Duality between Sobolev Spaces
11	Schwartz Representation Theorem Fundamental Solution of ∂x + i∂y Support of a Distribution; Distributions of Compact Support (Start)	Problem set 4 due
12	Compact Supports Convolution of Distributions supp(u*v) ⊂ supp(u)+ supp(v) if one, at least, has Compact Support Fundamental Solutions	Problem set 5 due
13	Singular Support, Hypoellipticity, Ellipticity - Parametrices for Elliptic Operators
14	Fundamental Solution of the Heat Operator, Hypoellipticity, Initial Value Problem Homogeneity The Distributions xz±, z ∈ C\(-N)
15	Distributions Supported at 0 Homogeneous Distributions of Order 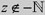 on the Line   Hadamard Regularization Cone Supports
16	Singular Support and Products Conic Support and Convolution
17	Wavefront Set Refines Singular Support Scattering Wavefront Set Product and Wavefront Set The Wave Equation	Problem set 6 due
18	Fundamental Solution of the Wave Equation Solution to the Cauchy Problem
19	Operators and Schwartz’ Kernel Theorem	Problem set 7 due
20-24	Lidskii’s Theorem Δ on the Torus Self-Adjointness of Δ+V Spectral Decomposition Wave Equation on the Torus Wave Equation on Torus with Potential Δ+V on Rn with V ∈ Cc(Rn)
25	Questions Trace as Integral of the Kernel over the Diagonal Microlocal Analysis