Course Meeting Times
Lectures: 2 sessions / week, 1.5 hours / session
Description
The main goal of this course is to give the students a solid foundation in the theory of elliptic and parabolic linear partial differential equations. We will begin with the theory of harmonic functions, and then study maximum principles for more general elliptic and parabolic equations. We will then discuss Schauder theory, that is, Hölder estimates for second derivatives of solutions to linear equations. If we have an equation of the form
Lu = f, or
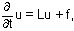
where L is a linear second order elliptic operator, then when does C^{alpha} regularity of f imply C^{2,alpha} regularity of u?
We will also discuss Sobolev spaces and the L^{p} theory for linear equations; the analogous question here is when does L^{p} regularity of f imply W^{2,p} regularity of u? We will then show some applications of this regularity theory of solutions to linear equations to the theory of nonlinear partial differential equations.
Prerequisite
Differential Analysis (18.155)
Textbook
Required Text
Jost, Jurgen. Partial Differential Equations. New York: Springer-Verlag, 2002. ISBN: 0387954287.
Recommended Text
Gilbarg, David, and Neil Trudinger. Elliptic Partial Differential Equations of Second Order. 2nd ed. Berlin: Springer-Verlag, 1983.
Grading
The basis for the course grade is class attendance and turning in homework assignments.










