Course Description
This course provides students with the basic analytical and computational tools of linear partial differential equations (PDEs) for practical applications in science engineering, including heat / diffusion, wave, and Poisson equations. Analytics emphasize the viewpoint of linear algebra and the analogy with finite …
This course provides students with the basic analytical and computational tools of linear partial differential equations (PDEs) for practical applications in science engineering, including heat / diffusion, wave, and Poisson equations. Analytics emphasize the viewpoint of linear algebra and the analogy with finite matrix problems. Numerics focus on finite-difference and finite-element techniques to reduce PDEs to matrix problems. The Julia Language (a free, open-source environment) is introduced and used in homework for simple examples.
Course Info
Instructor
Departments
Learning Resource Types
assignment_turned_in
Problem Sets with Solutions
grading
Exams with Solutions
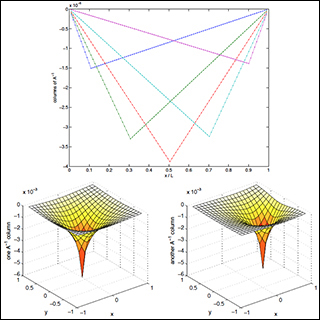
Colors of A\-1 where A is a discretized ∇2 with Dirichlet boundary conditions. Top: several columns in 1d (Ω = [0,L] = [0,1]). Bottom: two columns in 2d (Ω = [1,-1] x [-1,1]. In both 1d and 2d, the location of minimum corresponds to the index of the column: this is the effect of the unit-vector “source” or “force” = 1 at that position (and = 0 elsewhere). (Image by Steven G. Johnson.)








