Course Description
The course consists of a sampling of topics from algebraic combinatorics. The topics include the matrix-tree theorem and other applications of linear algebra, applications of commutative and exterior algebra to counting faces of simplicial complexes, and applications of algebra to tilings.
Course Info
Instructor
Departments
Learning Resource Types
assignment
Problem Sets
notes
Lecture Notes
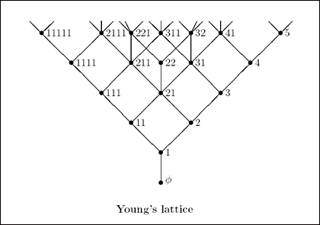
Young’s lattice Y, the poset of all partitions of all nonnegative integers, ordered by containment of their Young diagrams. (Image by Prof. Richard Stanley.)








