Course Description
This course provides an introduction to algebraic number theory. Topics covered include dedekind domains, unique factorization of prime ideals, number fields, splitting of primes, class group, lattice methods, finiteness of the class number, Dirichlet’s units theorem, local fields, ramification, discriminants.
Course Info
Instructor
Departments
Learning Resource Types
assignment
Problem Sets
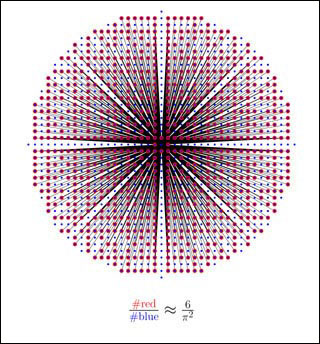
Relatively prime integers and zeta(2): The red dots are the coprime pairs of integers (x,y) with distance at most N (N = 20 in this picture) from the origin. They are connected to the origin by non-overlapping rays. The blue dots are all pairs of integers in the same disk. Their ratio tends to 1/zeta(2) = 6/pi^2 as N tends to infinity, where zeta(s) is the Riemann zeta funtion Sum_n (1/n^s). (Image by Prof. Abhinav Kumar.)








