Course Description
In this graduate-level course, we will be covering advanced topics in combinatorial optimization. We will start with non-bipartite matchings and cover many results extending the fundamental results of matchings, flows and matroids. The emphasis is on the derivation of purely combinatorial results, including min-max …
In this graduate-level course, we will be covering advanced topics in combinatorial optimization. We will start with non-bipartite matchings and cover many results extending the fundamental results of matchings, flows and matroids. The emphasis is on the derivation of purely combinatorial results, including min-max relations, and not so much on the corresponding algorithmic questions of how to find such objects. The intended audience consists of Ph.D. students interested in optimization, combinatorics, or combinatorial algorithms.
Course Info
Learning Resource Types
notes
Lecture Notes
assignment
Problem Sets
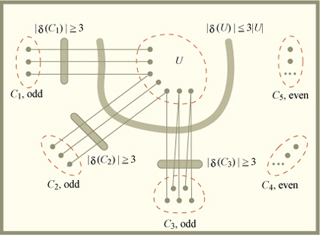
Illustration of the proof of Petersen’s theorem. (Image courtesy of Dan Stratila.)








