The project can be done by an individual student or in a team of two. The project is a design question, and you can use all the tools from the class to answer it. The last day of class will be project presentations.
Cell Differentiation and Design of Reprogramming Techniques
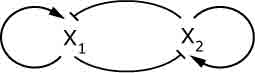
In this project, we are going to explore suitable models of cell differentiation for reprogramming purposes. Pluripotent stem cells can differentiate into a number of different cell types. It is known that a set of master genes control this differentiation process. Essentially, different cell types have the same genetic circuitry, but the specific steady state in which the circuit is determines the type of the cell. During cell differentiation, environmental stimuli drive the state of the circuit from one stable steady state to another, thus determining cell fate. The above diagram shows a key gene circuit motif involving two master regulator genes X1 and X2. The first objective of this project is to write down a mathematical model of the above circuitry satisfying specific characteristics known from experimental data. The second objective is to investigate robust “reprogramming strategies”.
- Write the simplest deterministic mathematical model of the above circuit and identify parameter conditions for which there are three stable steady states: S1 has low X2 and high X1 and corresponds to cell type 1; S2 has low X1 and high X2 and corresponds to cell type 2; S0 has comparable amounts of X1 and X2 and corresponds to the pluripotent cell state.
- The pluripotent cell state S0 is known to be not very robust to stochastic fluctuations and in fact it has been proposed that natural cell differentiation may be initially induced by stochastic fluctuations. To examine this, we will add noise to the deterministic model you developed in (1). Just assume additive Gaussian zero-mean noise with intensity I, which you can tune to address the following. Pick parameter values according to which when the system is initialized at S0, noise induces transitions to state S1 or S2. Make sure that instead, for the parameters that you picked, if you initialize the system at S1 or S2 noise is not capable of inducing transitions out of these states [this means roughly speaking that S1 and S2 have stronger stability properties than S0].
- Now, we examine reprogramming strategies, starting from the deterministic model you developed in (1) with the parameters that you determined in (2). In particular, for these parameters, determine the values of X1 and X2 in the three states S1, S2, and S0. Assume that the initial state of your circuit is in cell type 1 (S1). Determine an implementable design strategy that can revert the state S1 to state S0 exactly. Note that “exactly” means that we do not want to affect the values of X1 and X2 in state S0 permanently (only transiently is ok) and they should be exactly what you calculated above. This is important otherwise the cell type is not going to be exactly S0 but a variant that may even lead to pathological conditions. Hint: Transient overexpression of suitable genes is the current strategy used in cell reprogramming—however, how much each gene should be overexpressed to get to the desired state transition is a general question with no answer at this point. Also, note that you should provide an overexpression strategy that is robust to uncertainty: You will not be able to exactly overexpress a gene by a chosen amount, but only by that amount plus / minus some uncertainty. Your reprogramming strategy should work despite this unknown.
- Unfortunately, when you add back the noise with the intensity value you determined in (2), the state S0 that you latched into becomes subject to noise induced transitions, which can bring the cell type back to one of the two differentiated states. How can you counteract this? Is there a way for you to modify the control strategy in (3), perhaps through the addition of feedback, to mitigate the risk to differentiate back to an unwanted state? Investigate this.
Good luck!










