(b) Garner, et al. [1] claim that vacancies such as those induced by radiation damage produce an isotropic strain field. Prove that this is so, and explain whether this strain contribution is expected to contribute to plastic deformation via dislocation glide.
“If microscopy is employed to measure swelling, the only major strain detected is that due to void formation, a process known to be completely isotropic in its distribution of strain.” – Garner, et al.
Assuming a void is a spherical section of missing material, and assuming the void is not near any surface, there will be equal pressure from all sides from lattice atom repulsion in a cubic material. In the case of a single radiation-induced vacancy, it is likely that once the vacancy-interstitial pair is produced the interstitial easily diffuses away because the activation barrier for interstitial diffusion is much lower than that for vacancy diffusion. This leaves a vacancy in a (perfect) lattice. Each of its nearest neighbors is an equal distance away from the core of the vacancy, and therefore the lattice exerts equal pressure on the vacancy from all sides. This will strain the lattice isotropically in the direction of the vacancy.
As far as dislocation glide is concerned, one must look at the interactions of the stress fields produced by both the dislocation and the vacancy. A vacancy’s stress field is isotropically tensile, because the nearest neighbors (and next and so on) will relax into the vacant site a bit, stretching the lattice locally. A vacancy in the path of a dislocation may impede its glide motion, because a vacancy interacting with a dislocation can reduce the overall energy of the system by being absorbed by the half plane, producing one atom’s worth of dislocation climb. This correlates with experimental evidence of irradiation at low temperatures causing materials to become stiffer, for at a low temperature vacancies cannot easily diffuse from the sites in which they were created. This results in an increased fracture stress, implying that the motion of dislocations has been impeded.
(c) Garner, et al. [1] then discuss that ion bombardment at metal surfaces can lead to plastic deformation, e.g., via blistering bubbles of subsurface trapped gases. Treat such a blister as a spherical pressure vessel surrounded by your choice of metals discussed in the other two papers (this will set the mechanical properties of the material surrounding the gas bubble. Assume a subsurface bubble size of 0.5 micrometer radius, and determine the gas pressure required to initiate plastic deformation and consequent roughness for a bubble centered 1 micrometer beneath the initially flat surface.
Assumptions
Material around gas bubble can be modeled as a spherical pressure vessel. Outer radius of pressure vessel, ro, taken to be the center of gas bubble beneath the material surface
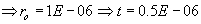
Since r/t < 10, must use “thick wall pressure vessel theory
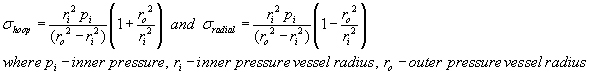
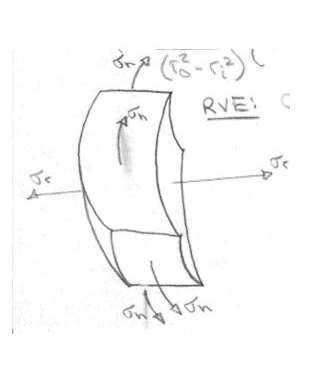
RVE: Radial and hoop stresses are the principal stresses
From von Mises yield criteria:
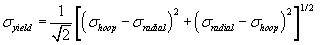
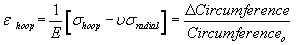
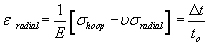
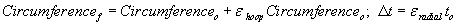
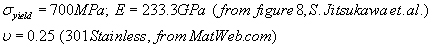
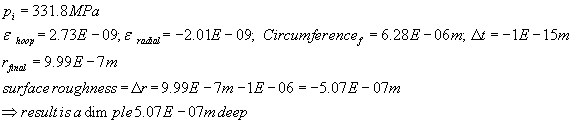
(d) Others have noted the superposition of lateral stress that contributes to plastic yielding at the surface. Explain the source and expected contribution of lateral stress for this metal.
The lateral stress would have the effect of squeezing the FCC and BCC grains in the steel. This lateral stress is due to thermal expansion, and is hydrostatic everywhere except near the surface, where it is essentially a two dimensional stress. The grains will therefore expand in the direction normal to the surface, and Fig. 1 in Garner, et al. shows that the FCC austenite grains are strained more than the BCC ferrite grains.
In addition, lateral stresses arise from voids created by ion bombardment. These are often due to gas pressure or to gas-free void nucleation, and are isotropically distributed throughout the plane parallel to the surface assuming constant normal irradiation. All these lateral stresses would have the effect of squeezing all the grains from four of its six sides, and these lateral stresses will cause the grains to expand into the free surface.
Mathematically, if the bulk of a crystal experiences a hydrostatic stress S from a combination of thermal expansion, void creation, gas bubble formation, and other processes, than at the surface σ1 = σ2 = S, and σ3 = 0. Therefore the lateral strain in the direction normal to the surface would be twice the Poisson’s ratio times the hydrostatic stress in the crystal bulk.
Reference
[1] Garner, F. A., and D. S. Gelles. “Irradiation Creep Mechanisms: An Experimental Perspective.” Journal of Nuclear Materials 159 (1988): 286-309.
Plasticity and fracture of microelectronic thin films/lines
Effects of multidimensional defects on III-V semiconductor mechanics
Defect nucleation in crystalline metals
Role of water in accelerated fracture of fiber optic glass
Carbon nanotube mechanics
Superelastic and superplastic alloys
Mechanical behavior of a virus
Effects of radiation on mechanical behavior of crystalline materials | Problem Set 2 | Problem Set 3 | Problem Set 5










