Course Description
The course covers the basic models and solution techniques for problems of sequential decision making under uncertainty (stochastic control). We will consider optimal control of a dynamical system over both a finite and an infinite number of stages. This includes systems with finite or infinite state spaces, as well as …
The course covers the basic models and solution techniques for problems of sequential decision making under uncertainty (stochastic control). We will consider optimal control of a dynamical system over both a finite and an infinite number of stages. This includes systems with finite or infinite state spaces, as well as perfectly or imperfectly observed systems. We will also discuss approximation methods for problems involving large state spaces. Applications of dynamic programming in a variety of fields will be covered in recitations.
Course Info
Instructor
Departments
Learning Resource Types
grading
Exams with Solutions
notes
Lecture Notes
theaters
Other Video
assignment
Problem Sets
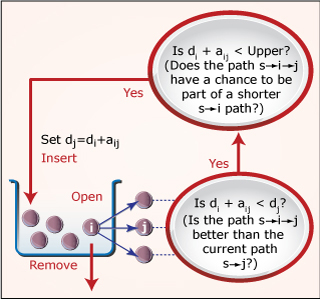
Label correcting methods for shortest paths. See Lecture 3 for more information. (Figure by MIT OpenCourseWare, adapted from course notes by Prof. Dimitri Bertsekas.)








