Course Description
This course provides students with the basic analytical and computational tools of linear partial differential equations (PDEs) for practical applications in science engineering, including heat / diffusion, wave, and Poisson equations. Analytics emphasize the viewpoint of linear algebra and the analogy with finite …
This course provides students with the basic analytical and computational tools of linear partial differential equations (PDEs) for practical applications in science engineering, including heat / diffusion, wave, and Poisson equations. Analytics emphasize the viewpoint of linear algebra and the analogy with finite matrix problems. Numerics focus on finite-difference and finite-element techniques to reduce PDEs to matrix problems. The Julia Language (a free, open-source environment) is introduced and used in homework for simple examples.
Course Info
Instructor
Departments
Learning Resource Types
grading
Exams with Solutions
assignment
Problem Sets
Problem Set Solutions
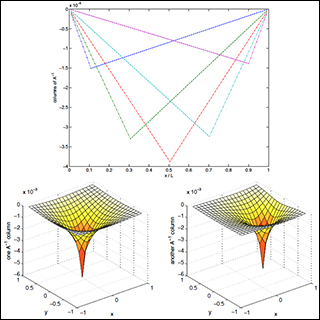
Colors of A\-1 where A is a discretized ∇2 with Dirichlet boundary conditions. Top: several columns in 1d (Ω = [0,L] = [0,1]). Bottom: two columns in 2d (Ω = [1,-1] x [-1,1]. In both 1d and 2d, the location of minimum corresponds to the index of the column: this is the effect of the unit-vector “source” or “force” = 1 at that position (and = 0 elsewhere). (Image by Steven G. Johnson.)
