« [Previous](/courses/8-03sc-physics-iii-vibrations-and-waves-fall-2016/) | Next »
Prerequisites
18.02 Multivariable Calculus and 8.02 Electricity and Magnetism.
This course is designed for students who are already familiar with the concepts taught in 8.01 Classical Mechanics as well as 8.02 Electricity and Magnetism. We also rely on fundamental mathematics principles taught in 18.01 Single Variable Calculus and 18.02 Multivariable Calculus, as well as some aspects of 18.06 Linear Algebra.
Course Overview
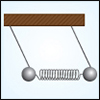
What are vibrations? Many physical systems vibrate or oscillate when something disrupts their equilibrium. Think of what happens when you pull a mass attached to a spring or push a pendulum in a certain direction. The mass bounces up and down. The pendulum swings back and forth. But even these simple phenomena can respond in complicated and counterintuitive ways when subjected to forces known in physics as damping and driving. Combining several pendulums or springs can lead to even more unexpected motions. In this course you will see how physics can describe these motions mathematically.
Extended physical systems that have been made to vibrate, like a string on a guitar, cannot return to their state of equilibrium without exerting forces on the area around them. These forces then lead to the phenomenon of waves, disturbances that propagate through a medium. The vibrating guitar string causes a sound wave to propagate through the medium of the air.
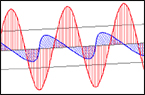
Among the most fascinating phenomena examined in the course are electromagnetic (EM) waves. EM waves have many properties similar to the waves we experience in everyday life, but the underlying physics of EM waves is profoundly different. Instead of a local disturbance exerting a force on adjoining regions, changing magnetic fields create electric fields (as quantified by Faraday’s Law), and changing electric fields create magnetic fields (as quantified by Maxwell’s extension of Ampere’s Law).
Course Goals
This course has two complementary goals. The first is to provide you with the concepts and mathematical tools necessary to understand and explain a broad range of vibrations and waves. This will allow you to gain a deeper appreciation for the true nature and beauty of phenomena like music and rainbows, which all of us observe or experience every day.
The second goal is to provide you with the skill of using a broad range of techniques that can greatly simplify the analysis and solution of complex systems. These techniques include complex numbers, combinations of oscillatory and exponentially decaying functions, resonance, normal modes, Cramer’s rule for solving several equations in several variables, boundary conditions, general wave equations, Fourier decomposition, dispersive and non-dispersive media, phase and group velocities, sound cavities and wave guides, polarization, Doppler effect, reflection and refraction, Fresnel’s equation for transmission and reflection, total internal reflection, constructive and destructive interference, and diffraction.
Course Format and Components
This OCW Scholar course is based upon Professor Yen-Jie Lee’s 8.03 Physics III: Vibrations and Waves course as taught on the MIT campus. It includes a complete set of 24 video lectures recorded at MIT in the Fall of 2016. Additional materials have been developed specifically for this OCW Scholar course, including:
- Lecture Notes aligned with the lecture videos
- Problem Sets (no solutions)
- Problem Solving Help Videos providing step-by-step solutions to sample problems
- Exams with Solutions
MIT students spend about 150-200 hours learning Vibrations and Waves in the on-campus version of this course. That number comes from a combination of attending lectures and recitations, and studying independently. It’s difficult to estimate how long it will take you to complete all of the modules in this particular course, but you can probably expect to spend 3 to 4 hours on practice problems, readings and assessment for each hour of lecture video you watch.
Required Textbook
Georgi, Howard. The Physics of Waves. Benjamin Cummings, 1992. ISBN: 9780136656210. Download the book (PDF - 5.5MB) (Courtesy of Howard Georgi. Used with permission.)
Suggested References
French, A. P. Vibrations and Waves. New York: W.W. Norton, 1980. ISBN: 9780393099362.
 Bekefi, George, and Alan H. Barrett. Electromagnetic Vibrations, Waves, and Radiation. MIT Press, 1977. ISBN: 9780262520478. [Preview with Google Books]
Bekefi, George, and Alan H. Barrett. Electromagnetic Vibrations, Waves, and Radiation. MIT Press, 1977. ISBN: 9780262520478. [Preview with Google Books]
« [Previous](/courses/8-03sc-physics-iii-vibrations-and-waves-fall-2016/) | Next »








