Course Description
The goal of these lectures is to provide an introduction to Fourier analysis. The first topic is Fourier series, in particular, the Gibbs phenomenon and the dependence of their convergence properties on the suitability method used. The second topic is the Fourier transform, first the L¹ theory and then, using Hermite …
The goal of these lectures is to provide an introduction to Fourier analysis. The first topic is Fourier series, in particular, the Gibbs phenomenon and the dependence of their convergence properties on the suitability method used. The second topic is the Fourier transform, first the L¹ theory and then, using Hermite functions, the L² theory. The third topic is L. Schwartz’s theory of tempered distributions. The fourth topic is the theory of weak convergence of probability measures and application to a derivation of the Lévy-Khinchine formula for the Fourier transform of infinitely divisible probability measures. The final topic is the elementary theory of singular integral operators, starting with the Hilbert transform and then using the method of rations to prove the Lᵖ boundedness of even Calderòn-Zygmund kernels.
Course Info
Instructor
Departments
Topics
Learning Resource Types
menu_book
Open Textbooks
notes
Lecture Notes
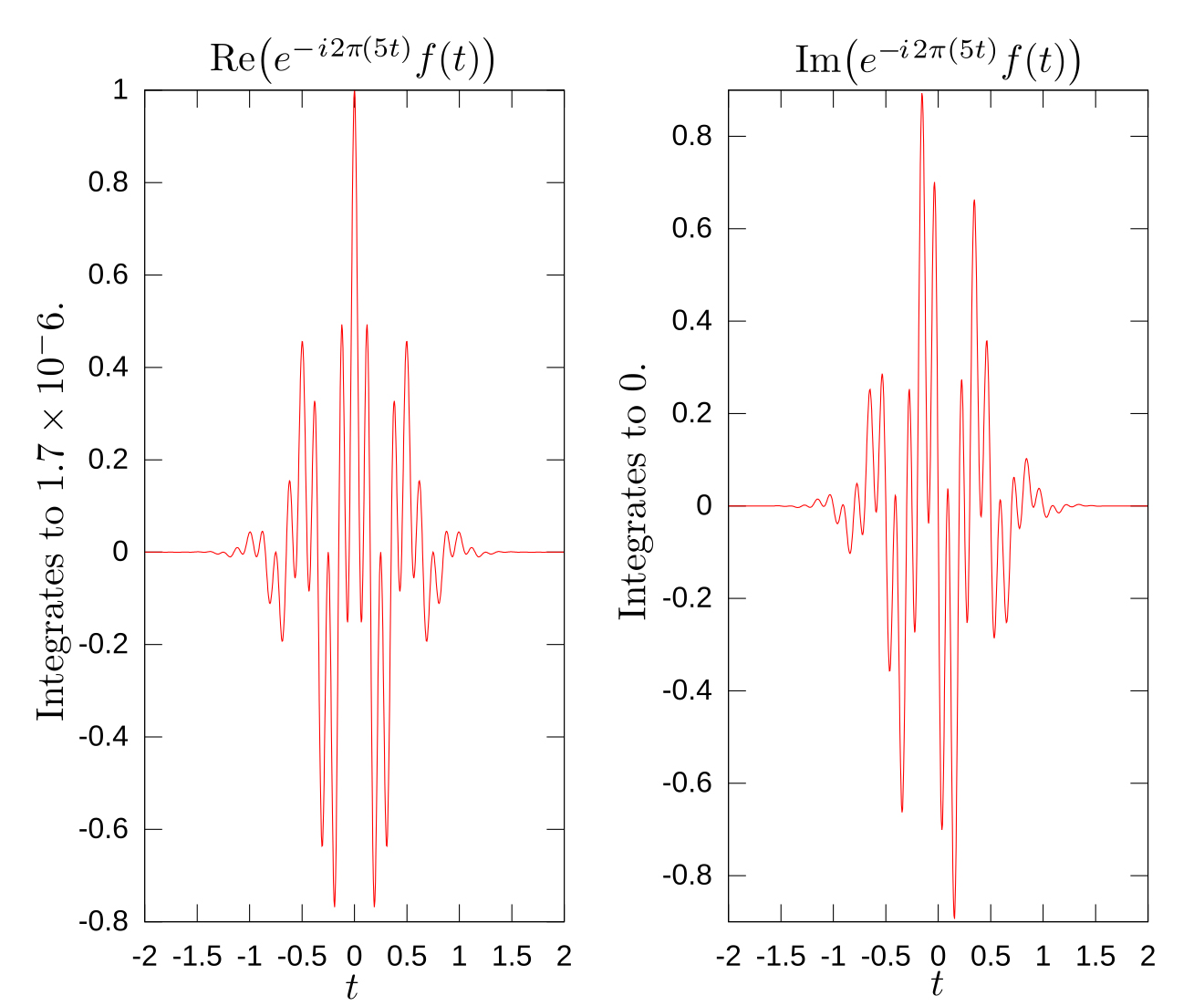
Real and imaginary parts of an integrand for the Fourier transform at 5 Hz. This image shows the real and imaginary parts of an oscillating function times the complex exponential with oscillating at a different rate. (Courtesy of Thenub314 on Wikipedia. License: CC BY.)










