|
Given two vectors v and w whose components are elements
of R, with the same number of components, we define their
dot product, written as v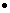 w
or (v, w) as the sum of the products of corresponding
components:  .
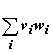Obvious facts: The dot product is linear in
v and in w and is symmetric between them. We define the length
of v to be the positive square root of (v, v); the
length of v is usually denoted by |v|
Wonderful Fact: The dot product v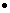w
is unaffected by rotation between any pair of components.
Exercises 3.1 Prove this statement. Solution
As a consequence of this fact, in evaluating v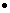w
we can rotate coordinates so that the first basis
vector is in the direction of v and the second one is perpendicular
to it in the vw plane.
Then v will have first two coordinates (|v|, 0) and if
the angle between v and w is  ,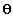
w will have (|w|cos,
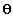|w|sin)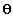
as its similarly defined coordinates.
The dot product vw
therefore is |v||w| cos,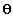
in this coordinates system and hence in any coordinate
system.
The fact that the dot product is linear in each of its
arguments is extremely important and valuable. It means that
you can apply the distributive law in either argument
to express the dot product of a sum or difference as the sum
or difference of the dot products.
Example
Exercises 3.2 Express the square of the area of a parallelogram
with sides v and w in terms of dot products. Solution
The dot product of
v and w divided by the magnitude of w, which
is |v|cos ,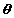
is called the component of v in the direction of
w.
The vector in the w direction having magnitude and
sign of |v|cos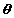
is called the projection of v on w.
The vector obtained by subtracting the projection of
v on w from v is called the projection
of v perpendicular to w or normal to w.(By
definition this projection has zero component in the direction
of w, and is therefore normal to w.)
Exercises:
3.3 Express the square of the component of v in the direction
of w in terms of dot products. Solution
3.4 Express the component of v perpendicular to w in terms
of dot products. Solution
3.5 Write out (v - w)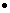(v
- w) using the linearity of the dot product in each of its
arguments. What famous law does this establish? Solution
Exercise 3.6 Express the projection of v on w in
terms of dot products and the vector w. Solution
|
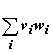