Parabolic approximation to a surface and local eigenframe.

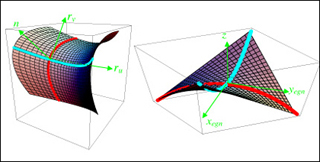
Parabolic approximation to a surface and local eigenframe. The surface on the left is a second-­order approximation of a surface at the point where the coordinate axes are drawn. The surface has a local normal at that point which is related to the cross product of the two tangents of the coordinate curves that cross at the that point. The three directions define a coordinate system. The coordinate system can be translated so that the origin lies at the point where the surface is expanded and rotated so that the normal n coincides with the z-axis as in the right hand curve. (Image by Prof. W. Craig Carter.)