Driven Harmonic Oscillators
Problem 1
A torsional oscillator comprises a cylinder with moment of inertia, \(I\), hanging from a light rod with torsional spring constant, \(\kappa\). The cylinder also experiences a drag torque equal to \(-\mu \dot \theta\), when moving with angular velocity \(\dot \theta\). The top of the rod is driven with angular displacement \(\phi(t) = \phi_0 \cos{\omega t}\).
- Find the steady-state solution for \(\theta(t)\).
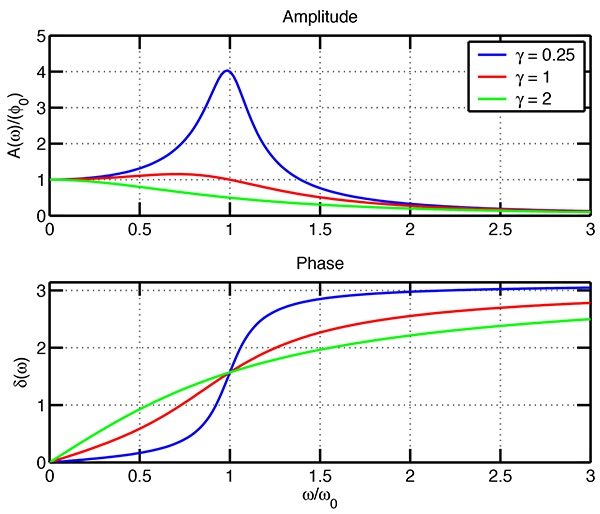
- Plot the amplitude \(A(\omega) \) and phase \(\delta(\omega)\) of your solution for \(\theta(t)\) in (1) as a function of \(\omega\). For your plot, assume that the natural frequency of oscillation of the system \(\omega_0 = 1\), and plot three curves on the same plot with \(\frac{\mu}{I} = 0.25\), 1 and 2. Label your curves to distinguish the three cases.
› View/Hide Answers
\begin{align*} \theta(t) &= \frac{\omega_0^2\,\phi_0}{\sqrt{\left(\omega_0^2 - \omega^2\right)^2 + \gamma^2\,\omega^2}}\,\cos\left({\omega\,t - \arctan{\left(\frac{\gamma\,\omega}{\left(\omega_0^2 -\omega^2\right)}\right)}}\right) \end{align*} \begin{align*} \text{where} \hspace{5mm} \gamma =\mu/I \hspace{5mm} \text{and} \hspace{5mm} \omega_0^2 = \kappa/I \end{align*}
\begin{align*} & A(\omega) = \frac{\omega_0^2\,\phi_0}{\sqrt{\left(\omega_0^2 - \omega^2\right)^2 + \gamma^2\,\omega^2}}\hspace{1mm}, \hspace{4mm} & \tan{\delta(\omega)} = \frac{\gamma\,\omega}{\left(\omega_0^2 -\omega^2\right)} \end{align*}
Problem 2
A capacitor (of capacitance C), a resistor (of resistance R) and an inductor (of inductance L) are connected to an AC voltage source \(V = V_0 \sin(\omega t)\) starting at \(t=0\) as shown in the diagram below.
Assuming that both the current and the charge of the capacitor are initially zero, determine the expression for \(V_C(t\ge0)\) with \(\omega=\omega_0=\dfrac{1}{\sqrt{LC}}\) and \(L < 4R^2C\).
› View/Hide Answer
\begin{align*} V_C(t\ge0) = V_{0}[-\dfrac{\omega_{0}}{\omega’}e^{-\frac{\gamma t}{2}} \sin(\omega’t) + \sin(\omega_{0}t)] \end{align*} \begin{align*} \text{where} \hspace{5mm} \omega’ = \sqrt{\frac{1}{LC} - \frac{1}{4R^2C^2}} \hspace{5mm} \text{and} \hspace{5mm} \gamma = \frac{1}{RC} \end{align*}








