Electromagnetic Waves in a Vacuum
Problem 1
Two parallel strips of metal of negligible resistance have width \( w \) and length \( D \). They are separated by a distance \( d \) with \( d \ll w \) and \( w \ll D \). At time \( t = 0 \) a constant potential difference, \( V_0 \), is applied across the two strips at the left end of the strips and kept at \( V_0 \) for all \( t >0 \). The system is shown in the figure below.

Choose some instant of time, \( t = T>0 \), such that the voltage across the two strips at the far end is still zero. You may ignore the fringe fields. At time \( t = T \):
- Plot the magnitude of the electric field, \( \mathbf{E} \), and magnetic field, \( \mathbf{B} \) (between the strips) as a function of the longitudinal position along the strips.
- What are the directions of the vectors \( \mathbf{E} \) and \( \mathbf{B} \)?
- Compute the power supplied by the voltage source.
› View/Hide Hint
You can do this problem either by transmission line analysis (inductance, capacitance per unit length, etc.) or by physical reasoning on how electromagnetic fields propagate between the plates (free space).
› View/Hide Answers
-
\( E_0 = \dfrac{V_0}{d}, \hspace{2mm} B_0 = \dfrac{E_0}{c} \), plots shown below.
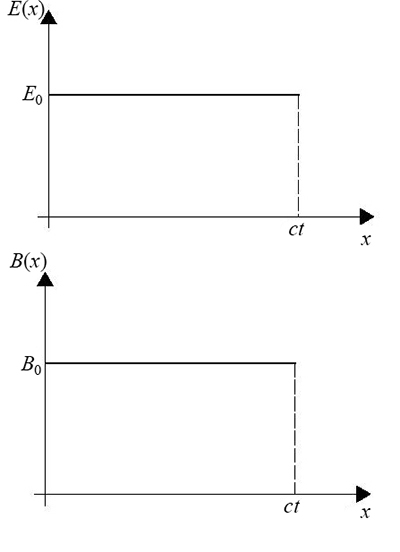
- \( \mathbf{E} \) points from upper to lower strip, \( \mathbf{B} \) is parallel to the strips (pointing into the paper).
- Power supplied by voltage source = \(\dfrac{V_0^2 w}{\mu_0 cd}\)
Problem 2
Sunlight with B-field \(\vec{B} = 10^{-6} (B_x, 2, 0) \cos ( \omega t - k_x x + k_y y)\) webers/m\(^2\), where \(k_x = 8\pi /a\), \(k_y = 6\pi/a\) and a = 2500 nanometers, shines on a mirror-like polar ice lying in the \(x\)-\(z\) plane. The area of the ice is 100,000 square kilometers.
- Find \(B_x\), the direction, the wavelength and the frequency of the incident sunshine;
- Find the E-field of the incident sunshine;
- Find the Poynting vector of the incident sunshine;
- Find the reflected E-field;
› View/Hide Hint
What are the boundary conditions at the surface of a perfect conductor?
- Find the total E-field;
- Due to global warming, this piece of ice has just melted, exposing the totally absorbing black rocks underneath. How much additional energy per second is the Earth absorbing due to this melted ice? How does it compare with the average electrical power consumption of the world (about four times the US power consumption, which is the average power consumption per person times the US population)?
› View/Hide Answers
- The direction \(\hat{n} = (4/5,-3/5,0)\); the wavelength is \(\lambda = a/5 = 500 \) nm; the frequency of the incident sunshine \(f=c/\lambda = 6\cdot 10^{14} \) Hz; and \(B_x = 3/2\), thus \(\vec{B} = 2.5\cdot 10^{-6} (3/5,4/5,0)\cos (\omega t - k_x x + k_y y) \) webers/m\(^2\).
- The incident E-field = \(-c \hat{k}\times \vec{B} = 7.5\times 10^2 (0,0,-1) \cos(\omega t - k_x x + k_y y)\) Newtons/Coulomb
- The Poynting vector of the incident light: \begin{eqnarray} \nonumber \vec{S} &=& 1.5 \times 10^3 \cos^2(\omega t - k_x x +k_y y)\hat{n} ~\text{Watts/m}^2 \\ \nonumber \text{<}cos^2(\omega t - k_x x +k_y y)\text{>} &=& 0.5 \\ \nonumber \text{and so} \hspace{22mm} \text{<}S\text{>} &=& 7.5\times 10^2 ~\text{Watts/m}^2 \end{eqnarray}
- The reflected E-field = \(7.5\times 10^2 (0,0,1)\cos(\omega t -k_x x - k_y y)\) Newtons/Coulomb
- The total E-field = \(1.5 \times 10^3 (0,0,1) \sin (\omega t -k_xx)\sin(k_yy)\) Newtons/Coulomb, i.e. a propagating wave in the \(x\) direction and a standing wave in the \(y\) direction;
- The additional energy per second absorbed by the Earth is \begin{align*} \vec{S}\cdot\vec{A} = 4.5\times 10^{13} ~\text{Watts} \end{align*} which is much bigger than the \(\sim 2\times 10^{12}\) Watts of the average electrical power consumption of the world (\( \sim 10\) billion people world-wide times 100 Watts/person, or see e.g. Orders of magnitude (power)), so global warming will accelerate faster and faster, as more and more ice melts.










