Traveling Waves without Damping
Problem 1
There is a horizontal taut ideal string with a length of 8 meters, fixed at the left end (\(x=0\)) and attached to a massless ring free to slide on a frictionless rod on the right end at \(x=8\ m\). The string has a mass of 0.5 kilograms and tension of 4 Newtons, assumed to be constant.
At \(t=0\) the profiles of the transverse displacement \(y\) and transverse velocity, \( \dfrac{\partial y}{\partial t} \), of the string are as shown below.
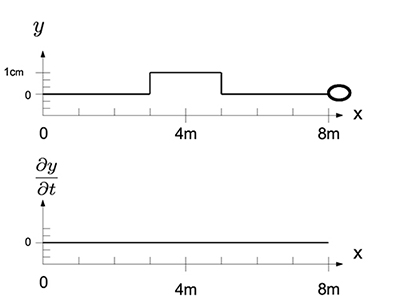
On the graph below, sketch the shape of the string at \(t = 0.25\) sec, and at \(t = 1\) sec. Make sure you indicate the scale for \(y\).
› View/Hide Hint
This type of problem is done most easily by decomposing waveforms into superposition of progressive waves.
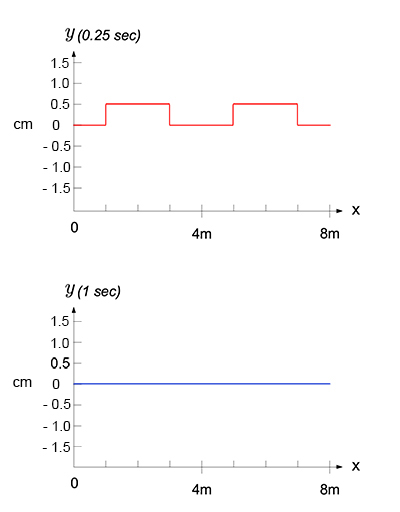
View the answer below:
Problem 2
Voltage, current waves propagating on a transmission line undergo reflection and transmission at a junction between lines with different characteristics. If one considers two transmission lines, joined at \(x=0\), with inductance and capacitance (per unit length) of \(L\) and \(C\) for \(x < 0\), and \(L\) and \(C/4\) for \(x > 0\), then the characteristic phase velocity and impedance increase by a factor of 2 across the junction at \(x=0\). Show that this results in transmission and reflected voltage amplitudes (relative to the incoming pulse) of
\begin{eqnarray} \nonumber T &=& \frac{4}{3} \\ \nonumber R &=& \frac{1}{3} \end{eqnarray}
Also show that, in spite of the increased amplitude of transmission and the existence of a reflected pulse, energy is conserved in this system.
› View/Hide Hint
Show that the sum of the power flowing in the transmitted and reflected pulses adds up, exactly, to the incident power.








