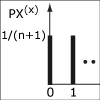
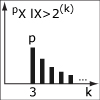
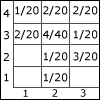
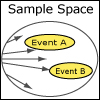
This unit covers the basic framework of probability theory: probabilistic models, conditional probabilities, independence, the Bayes’ rule, and counting methods. In addition, it introduces discrete random variables and the concept of the Probability Mass Function (PMF) used to describe the probability distribution of one or several random variables. Finally, it defines the concepts of expectation and variance, and their basic properties.
|
|
Looking for something specific in this course? The Resource Index compiles links to most course resources in a single page.