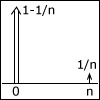
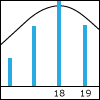
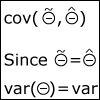In this section, we start with a discussion of limit theorems: the weak law of large numbers and the central limit theorem. We then introduce the subject of inference (estimation and hypothesis testing), from two alternative viewpoints: first, Bayesian inference, which relies on a prior distribution for unknown quantities and on the Bayes rule to incorporate new evidence; and, second, classical inference, in which no probabilistic assumptions are made on the unknown quantities and instead relies heavily on the laws of large numbers to provide statistical guarantees, e.g., in the form of confidence intervals.
Looking for something specific in this course? The Resource Index compiles links to most course resources in a single page.