First published in 1991 by Wellesley-Cambridge Press, this updated 3rd edition of the book is a useful resource for educators and self-learners alike. It is well organized, covers single variable and multivariable calculus in depth, and is rich with applications. There is also an online Instructor’s Manual and a student Study Guide.
The complete textbook (PDF) is also available as a single file.
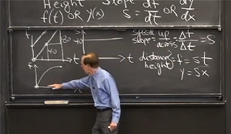
|
Highlights of Calculus MIT Professor Gilbert Strang has created a series of videos to show ways in which calculus is important in our lives. The videos, which include real-life examples to illustrate the concepts, are ideal for high school students, college students, and anyone interested in learning the basics of calculus. › Watch the videos |
Textbook Components
Chapter 0: Highlights of Calculus (PDF)
0.1 Distance and Speed // Height and Slope
0.2 The Changing Slope of \(y=x^2\) and \(y=x^n\)
0.3 The Exponential \(y=e^x\)
0.4 Video Summaries and Practice Problems
0.5 Graphs and Graphing Calculators
Chapter 1: Introduction to Calculus (PDF)
1.1 Velocity and Distance
1.2 Calculus Without Limits
1.3 The Velocity at an Instant
1.4 Circular Motion
1.5 A Review of Trigonometry
1.6 A Thousand Points of Light
2.1 The Derivative of a Function
2.2 Powers and Polynomials
2.3 The Slope and the Tangent Line
2.4 Derivative of the Sine and Cosine
2.5 The Product and Quotient and Power Rules
2.6 Limits
2.7 Continuous Functions
Chapter 3: Applications of the Derivative (PDF)
3.1 Linear Approximation
3.2 Maximum and Minimum Problems
3.3 Second Derivatives: Bending and Acceleration
3.4 Graphs
3.5 Parabolas, Ellipses, and Hyperbolas
3.6 Iterations \(x_{n+1}=F(x_n)\)
3.7 Newton’s Method (and Chaos)
3.8 The Mean Value Theorem and 1’Hôpital’s Rule
Chapter 4: Derivatives by the Chain Rule (PDF)
4.1 The Chain Rule
4.2 Implicit Differentiation and Related Rates
4.3 Inverse Functions and Their Derivatives
4.4 Inverses of Trigonometric Functions
5.1 The Idea of an Integral
5.2 Antiderivatives
5.3 Summation versus Integration
5.4 Indefinite Integrals and Substitutions
5.5 The Definite Integral
5.6 Properties of the Integral and Average Value
5.7 The Fundamental Theorem and Its Applications
5.8 Numerical Integration
Chapter 6: Exponentials and Logarithms (PDF)
6.1 An Overview
6.2 The Exponential \(e^x\)
6.3 Growth and Decay in Science and Economics
6.4 Logarithms
6.5 Separable Equations Including the Logistic Equation
6.6 Powers Instead of Exponentials
6.7 Hyperbolic Functions
Chapter 7: Techniques of Integration (PDF)
7.1 Integration by Parts
7.2 Trigonometric Integrals
7.3 Trigonometric Substitutions
7.4 Partial Fractions
7.5 Improper Integrals
Chapter 8: Applications of the Integral (PDF)
8.1 Areas and Volumes by Slices
8.2 Length of a Plane Curve
8.3 Area of a Surface of Revolution
8.4 Probability and Calculus
8.5 Masses and Moments
8.6 Force, Work, and Energy
Chapter 9: Polar Coordinates and Complex Numbers (PDF)
9.1 Polar Coordinates
9.2 Polar Equations and Graphs
9.3 Slope, Length, and Area for Polar Curves
9.4 Complex Numbers
Chapter 10: Infinite Series (PDF)
10.1 The Geometric Series
10.2 Convergence Tests: Positive Series
10.3 Convergence Tests: All Series
10.4 The Taylor Series for \(e^x\), \(\sin{x}\), and \(\cos{x}\)
10.5 Power Series
Chapter 11: Vectors and Matrices (PDF)
11.1 Vectors and Dot Products
11.2 Planes and Projections
11.3 Cross Products and Determinants
11.4 Matrices and Linear Equations
11.5 Linear Algebra
Chapter 12: Motion Along a Curve (PDF)
12.1 The Position Vector
12.2 Plane Motion: Projectiles and Cycloids
12.3 Curvature and Normal Vector
12.4 Polar Coordinates and Planetary Motion
Chapter 13: Partial Derivatives (PDF)
13.1 Surface and Level Curves
13.2 Partial Derivatives
13.3 Tangent Planes and Linear Approximations
13.4 Directional Derivatives and Gradients
13.5 The Chain Rule
13.6 Maxima, Minima, and Saddle Points
13.7 Constraints and Lagrange Multipliers
Chapter 14: Multiple Integrals (PDF)
14.1 Double Integrals
14.2 Changing to Better Coordinates
14.3 Triple Integrals
14.4 Cylindrical and Spherical Coordinates
Chapter 15: Vector Calculus (PDF)
15.1 Vector Fields
15.2 Line Integrals
15.3 Green’s Theorem
15.4 Surface Integrals
15.5 The Divergence Theorem
15.6 Stokes’ Theorem and the Curl of F








