Topics
- Strategic substitutes
- Strategic complements (local network effects, continued)
- Subgame perfect equillibrium
- Rubinstein’s bargaining game
Strategic Substitutes
If other players act more aggressively, you have incentive to act less aggressively, and vice versa.
Strategic Complements
If other players act more aggressively, you have incentive to act more aggressively, and vice versa.
Example: Playing Sports with Friends
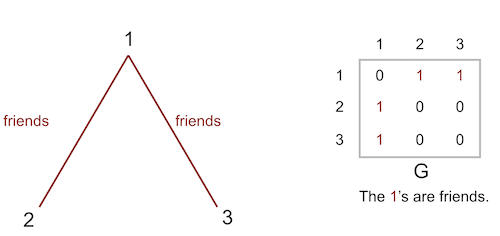
- N = {1, 2, 3}
- Si = ℝ+ = [0, ∞)
- ui(xi, x-i, δ, G) = xi — ½ xi2 + δ∑(j≠i) gij xi xj
- Where δ is the degree of complementarity (δ ≥ 0).
- Best response of player i:
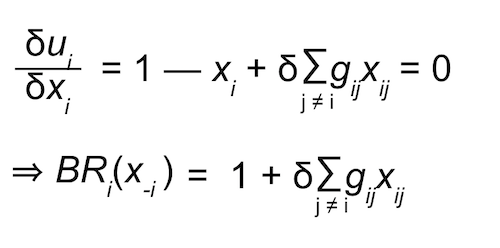
- Collectively, BRi(x-i) = 𝟙 + δG𝕏.
- The equilibrium (fixed point) is 𝕏* = (I — δG)-1𝟙.
Subgame Perfect Equilibrium
Nash equlibrium only requires mutual optimality:
- Issue 1: In dynamic games, cannot change the strategy you have taken in the past.
- Subgame perfect equilibrium (SPE).
- Issue 2: Some players may know what other players don’t.
- (Perfect) Bayesian Nash equilibrium.
Example: Battle of the Sexes
| Shopping | Football | |
|---|---|---|
| Shopping | (3, 2) | (0, 0) |
| Football | (0, 0) | (2, 3) |
- Where (3, 2) and (2, 3) are the two Nash equalibirums.
Suppose the girl wakes up very early. Then, she can wait at Starbucks in the mall.
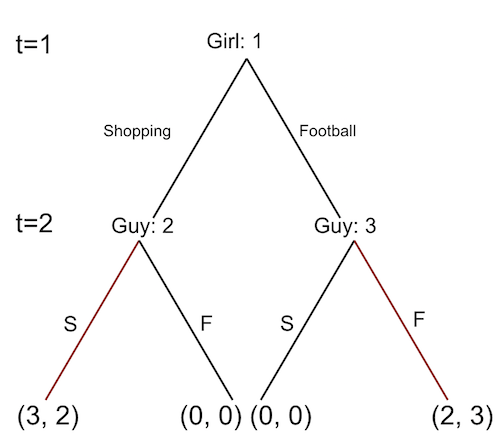
Then, (3, 2) is the unique SPE. The guy claiming that he’ll definitely go to football no matter what is an “empty threat.”
Rubinstein’s Bargaining Game
- Seller (player 1) does not value the good: v1 = 0.
- Buyer (player 2) values the good: v2 = 1.
Question: How is the price determined?
Answer: Many models, e.g. take-it-or-leave-it-offer. Rubenstein’s is important because it can generate price ≈ ½ without altruism.
Suppose they make alternating offers of prices until either accepts an offer. What is the SPE?
When traded at price p:
- Player 1 receives payoff p.
- Player 2 receives payoff q := 1 — p.
Trick: Let ͟p and p̅ be the minimum and maximum payoffs 1 can receive in his turn. Similarly, define ͟q and q̅.
- In 1’s turn, since any offer above δ q̅ is accepted, p ≥ 1 — δq̅.
- Since any offer below δ͟q is rejected, p̅ ≤ 1 — δ͟q.
- Similarly, in 2’s turn, we get ͟q ≥ 1 — δ p̅ and q̅ ≤ 1 — δ͟p.
- Combining, we get:
- p ≥ 1 — δq̅ ≥ 1 — δ(1 — δ͟p) ⇒ ͟p ≥ (1 — δ)/(1 — δ2) = 1/(1 + δ).
- p̅ ≤ 1 — δ͟q ≤ 1 — δ(1 — δp̅) ⇒ p̅ ≤ (1 — δ)/(1 — δ2) = 1/(1 + δ).
- Thus, p = p̅ = 1/(1 + δ) and ͟q = q̅ = 1/(1 + δ).
Bottom line: If there is any SPE, 1’s payoff at t=odd should be 1/(1 + δ) and 2’s payoff at t=even be 1/(1 + δ).
Indeed, this equilibrium payoff profile is attainable if and only if they take the following strategies:
- Player 1: At t=odd, offer p = 1(1 + δ)
and at t=even, accept any offer above p = δ/(1 + δ). - Player 2: At t=odd, accept any offer above q = δ/(1 + δ)
and at t=even, offer q = 1/(1 + δ).
On the equilibrium path, 1 offers p = 1/(1 + δ) and 2 immediately accepts it; end of game.








