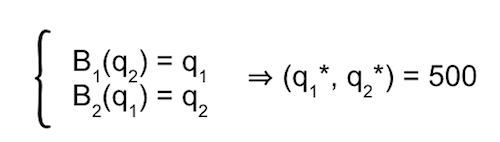Networks

Recitation 7 Notes

Topics

• What is a game?
• Normal form games
• Equilibria

Games

Why game theory? Games on networks!

Ex. congestion, international trade, Amazon’s new office location, peer effects in school learning, deciding state taxes.       
A game is a representation of strategic interaction. 

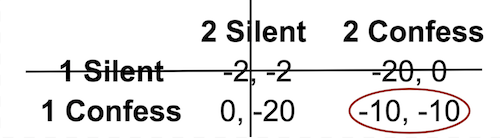
Example: Prisoner’s Dilemma

	2 Silent	2 Confess
1 Silent	-2, -2	-20, 0
1 Confess	0, -20	-10, -10

Example: Cournot Competition

How many iPhones should Apple produce?

• Apple produces q₁ iPhones at marginal cost $500.
• Samsung produces q₂ Galaxies at marginal cost $500.
• Price given by inverse demand P = 2000 — Q, Q = q₁ + q
• Apple’s profit given by Pq₁ — $500 * q
• Samsung’s profit given by Pq₂ — $500 * q

Normal Form Games

Formally, a game consists of 3 elements:

1. The set of players N.
2. The sets of strategies {Si}i∈N.
3. The sets of payoffs {ui: S → ℝ }i∈N.

Example: Prisoner’s Dilemma

• N = {1, 2} 
• S₁ = {silent, confess}, S₂ = {silent, confess}
• u₁ : S₁ * S₂ → ℝ and u₂ : S₁ * S₂  → ℝ are given by the table, where u₁ is red and u₂ is blue.

	2 Silent	2 Confess
1 Silent	-2, -2	-20, 0
1 Confess	0, -20	-10, -10

Example: Cournot Competition

• N = {1, 2}
• S₁ = [0, ∞), S_2 = [0, ∞)
  • We ignore that q must be integers.
• u₁ : S → ℝ and u₂: S → ℝ given by       
  u_i (q₁, q₂) = (P — $500)q₁ = ($2000 — q₁ — q₂ — $500)q_i

In many cases, the sets of strategies have some structure:

1. Simultaneous games (penalty kicks in soccer).
2. Repeated games (Libor rate manipulation scandal).
3. Sequential games (how should US respond to china’s tariffs?).

What happens when there is a game-like situation?        
There are many variations…

• Weak prediction: “Dominated strategies are never played.”
• Strong prediction: “Mutually optimal strategies are played.”

Elimination of strictly dominated strategies

Example: Prisoner’s Dilemma

 

 

Example: Battle of the Sexes

No elimination needed.

Equilibria

Nash equilibrium - A state with no incentive to deviate that can be sustained.

Given the opponents’ strategies, what would you do?       
“Best response correspondence” B_i : S_-i → S_i

• B_girl(musical) = {musical}
• B_girl(soccer) = {soccer}
• B_boy(musical) = {musical}
• B_boy(soccer) = {soccer}

⇒ (M,M) and (S,S) are mutually optimal; “nash equilibria.”

When the best response correspondence only has one element, we may instead use the best response function (B_girl(musical) = musical).

Example: Cournot Competition

Given Samsung’s production q₂, Apple wants to maximize its profits

 

u₁(q₁, q₂)=(1500 — q₁ — q₂)q

_{\n<section data-uuid=}

That is, B₁(q₂) = ½(1500 — q₂). Similarly, B₂(q₁)= ½(1500 — q₂).

Nash equilibrium is the fixed point: