Networks

Recitation 12 Notes

Topics

• Bargaining on Networks
• Contagion Models
• Mean-Field Approximation

Recall

• Take-it-or-leave-it offer:
  • One party makes an offer. 
    Then, the other party accepts or rejects it. 
    Game end.
  • The proposer takes all the surplus. 
• Rubinstein’s bargaining:
  • One party makes an offer. 
    The other party accepts or rejects. 
    If rejected, he makes a counter offer. 
    Continue until a party accepts.
  • The first proposer takes 1/(1 + δ). The offeree takes δ/(1 + δ).

Bargaining on Networks

What if there are two sellers?

• Take-it-or-leave-it offer:
  • If S₁ offers p, S₂ has incentive to offer p — ε.
  • Even if sellers make (simultaneous) offers, they receive 0. The buyer receives 1.
• Rubinstein’s bargaining:
  • If S₁ offers 1/(1 + δ), S₂ has incentive to offer 1/(1 + δ) — ε.
  • Again, the sellers receive 0, the buyer takes it all. 

Contagion Models

Recall games with externalities

• N = [0, 1]
• S_i = {Adopt, Not Adopt}

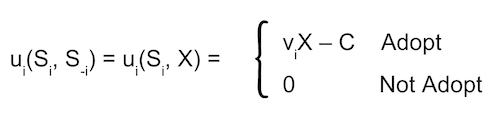
• Where X is the share of adoption. 

This has externalities, but network structure doesn’t matter. In reality, you may register for Instagram not only because it is popular, but also because your friends have it. 

Consider undirected graph (V, E), N(i) ⊂ V 
Where V are vertices, E are edges, and N is the set of neighbors of vertex i ∈ V.

• N = V
• S_i = {Adopt, Not Adopt} = {1, 0}.

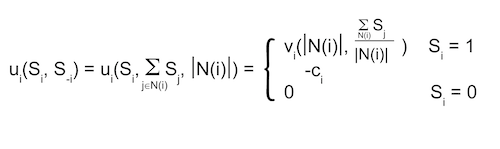
Example

• Too complicated to solve (many-body problem).
• Nor do we care about particular solution on particular networks. Often concerned with particular degree distribution, but not finer details.
• Mean-field approximation to solve for stationary equation. 

To solve:

1. Consider random graph with the degree distribution and fix some neighbor adoption probability X. 
2. Obtain best response strategy given X and compute adoption share X̂.
3. Derive fixed point. 

Example

Let N = V = [0, 1] and 

 

 

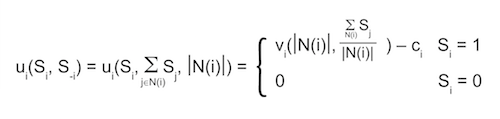
• Agents are heterogeneous c_i ~ F(0, 1).
• Degree distribution d_i ~ D.

To solve:

1. Fix some X. Pick agent i randomly.
2. i with c_i and d_i would adopt if

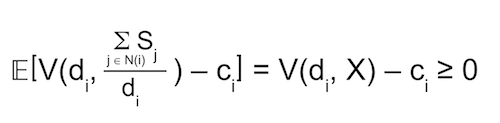
1. Since c_i ~ F[0, 1], the probability that a random person with degree d_i (but unknown c_i) adopts is F(V(d_i, X)). Since d_i ~ D, we have the share of adoption 𝔼_D[F(V(d_i, X))] . From here, we can compute the neighbor adoption share X̂.