Networks

Recitation 8 Notes

Topics

• Review
• Congestion Games
• Potential Games

Recap from Last Week

A game consists of 3 elements:

1. Set of players N
2. Sets of strategies {S_i}_i∈N
3. Sets of payoffs {u_i}_i∈N

Given a game, what do we do?

1. Maximize the sum of everyone’s payoff.
   • Socially optimal outcome (what we want to happen).
2. Maximize individual’s payoff conditional on everyone else’s strategy and find a fixed point.
   • Nash equilibrium (what we think will happen).

1 & 2 are often different because there are strategic interactions and individual incentives are unaligned. 

Some games have useful structures, which impose useful restrictions on {S_i} and {u_i}.

• Dynamic games
• Games on networks

Congestion Games

Paths are labeled (edge, traffic, cost/duration):

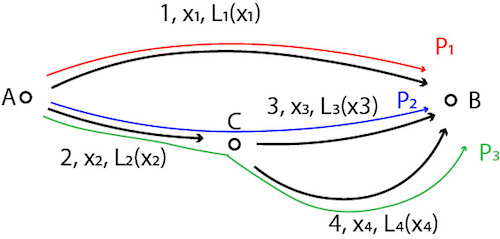
• Directed network (J, E) = ({A, B, C}, {1, 2, 3, 4}).
• Set of paths P = {p₁, p₂, p₃} = {(1), (2,3), (2,4)}.
• Traffic on paths {x_p1, x_p2, x_p3} = {x₁, x₃, x₄}.
• Total (social) cost: x₁*L₁(x₁) + x₂*L₂(x₂) + x₃*L₃(x₃) + x₄*L₄(x₄).
  • Minimizing this with respect to x₁, … x₄ gives socially optimal traffic.

As a game, this can be written:

• N = [0, 1]
• S_i = {p₁, p₂, p₃}
• u_i(P_i, everyone else’s strategy) = u_i(P_i, x₁…x₄)

However, each individual driver incurs:

• L₁(x₁) if he takes p_1.
• L₂(x₂) + L₃(x₃) if he takes p
• L₂(x₂) + L₄(x₄) if he takes p_3.

So, his best response correspondence is to choose a path that gives minimum individual cost.

• In equilibrium, we must have L₁(x₁) = L₂(x₂) + L₃(x₃) = L₂(x₂) + L₄(x₄).

Example:

Paths are labeled (edge/path, traffic, individual cost):

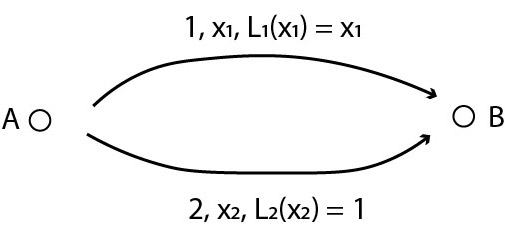
• Model constraint: x₁ + x₂ = 1.
• Total cost: x₁*L₁(x₁) + x₂*L₂(x₂) = x₁² + x₂ = x₁² + (1 — x₁) = (x₁ — ½)² + ¾.
• Socially optimal traffic: (x₁^S, x₂^S) = (½ , ½).

Each individual choose path with lower cost, so in equilibrium:

• L₁(x₁^E) = L₂(x₂^E), so (x₁^E, x₂^E) = (1, 0).
• Equilibrium total cost is x₁^E*L₁(x₁^E) + x₂^E*L₂(x₂^E) = 1 ≥ ¾.

How to solve this? 

1. Impose toll C on p₁.
2. Then, u_i(p₁, x₁, x₂) = x₁ + C.
3. We want L₁(x_1S) + C = L₂(x₂^S).
4. C = ½.

Potential Games

In physics, particles move along the unique potential field.

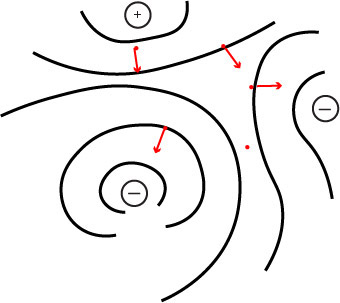
In society, people move along their own incentives.

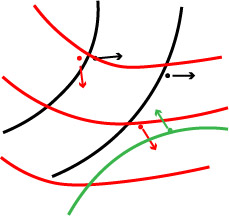
However, there are cases where people’s incentives are so similar that they move as if there is a unique potential field.

Example: Traffic Congestion

Definition: A game is an exact potential game if there is exists Φ (unique potential field) such that:

• u_i(S_i, S_-i) — u_i(S_i’, S_-i) = Φ(S_i, S_-i) — Φ(S_i’, S_i).
• That is, i’s incentive matches the potential’s gradient.