A pulley of mass \(\displaystyle m_ p\), radius \(\displaystyle R\), and moment of inertia about its center of mass \(\displaystyle I_{cm}\), is attached to the edge of a table. An inextensible string of negligible mass is wrapped around the pulley and attached on one end to block 1 that hangs over the edge of the table. The other end of the string is attached to block 2 which slides along a table. The coefficient of sliding friction between the table and the block 2 is \(\displaystyle \mu _ k\). Block 1 has mass \(\displaystyle m_1\) and block 2 has mass \(\displaystyle m_2\), with \(\displaystyle m_1>\mu _ k m_2\). At time \(\displaystyle t=0\), the blocks are released from rest. At time \(\displaystyle t=t_1\), block 1 hits the ground. Let \(\displaystyle g\) denote the gravitational constant.
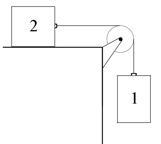
Find the direction and magnitude of the acceleration of the block 1 hanging over the edge of the table. The positive direction is chosen to be downward.








