Differential Equations

Matrix Exponentials

« Previous | Next »

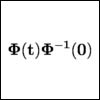
In this session we will learn the basic linear theory for systems. We will also see how we can write the solutions to both homogeneous and inhomogeneous systems efficiently by using a matrix form, called the fundamental matrix, and then matrix-vector algebra.

Session Activities

Read the course notes:

• Matrix Exponentials: Introduction (PDF)

Watch the lecture video clip:

• Theory of Systems

Read the course notes:

• General Linear ODE Systems and Independent Solutions (PDF)
• The Existence and Uniqueness Theorem for Linear Systems (PDF)
• The Wronskian (PDF)
• Existence and Uniqueness and Superposition in the General Case (PDF)

Watch the lecture video clip:

• Fundamental Matrices

Read the course notes:

• Fundamental Matrices (PDF)
• The Normalized Fundamental Matrix (PDF)

Watch the lecture video clips:

• The Matrix Exponential I
• The Matrix Exponential II

Read the course notes:

• The Exponential Matrix (PDF)

Watch the lecture video clips:

• Example: Solving a System with the Matrix Exponential
• Calculating the Exponential Matrix
• Variation of Parameters

Read the course notes:

• Inhomogeneous Case: Variation of Parameters Formula (PDF)

Watch the problem solving video:

• Matrix Exponentials

Complete the practice problems:

• Practice Problems 35 (PDF)
• Practice Problems 35 Solutions (PDF)

Check Yourself

Complete the problem sets:

• Problem Set Part I Problems (PDF)
• Problem Set Part I Solutions (PDF)
• Problem Set Part II Problems (PDF)
• Problem Set Part II Solutions (PDF)

Session Activities

Watch the lecture video clip:

• Decoupling

« Previous | Next »