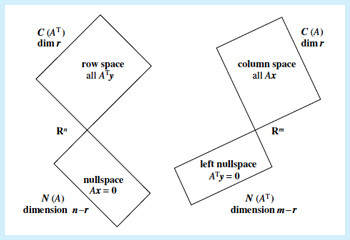
The big picture of linear algebra: Four Fundamental Subspaces.
Mathematics is a tool for describing the world around us. Linear equations give some of the simplest descriptions, and systems of linear equations are made by combining several descriptions.
In this unit we write systems of linear equations in the matrix form Ax = b. We explore how the properties of A and b determine the solutions x (if any exist) and pay particular attention to the solutions to Ax = 0. For a given matrix A we ask which b can be written in the form Ax.
Looking for something specific in this course? The Resource Index compiles links to most course resources in a single page.








