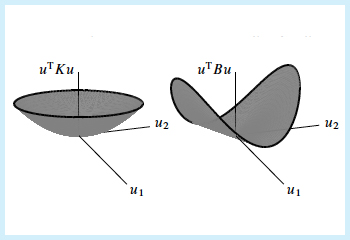
Positive definite and semidefinite: graphs of x’Ax.
In this unit we discuss matrices with special properties – symmetric, possibly complex, and positive definite. The central topic of this unit is converting matrices to nice form (diagonal or nearly-diagonal) through multiplication by other matrices. Generally, this process requires some knowledge of the eigenvectors and eigenvalues of the matrix.
Looking for something specific in this course? The Resource Index compiles links to most course resources in a single page.








