Session Overview
|
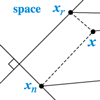
Vectors are easier to understand when they’re described in terms of orthogonal bases. In addition, the Four Fundamental Subspaces are orthogonal to each other in pairs. If A is a rectangular matrix, Ax = b is often unsolvable. The matrix ATA will help us find a vector x̂ that comes as close as possible to solving Ax = b. |
Session Activities
Lecture Video and Summary
- Watch the video lecture Orthogonal Vectors and Subspaces
- Read the accompanying lecture summary (PDF)
- Lecture video transcript (PDF)
Suggested Reading
- Read Section 4.1 in the 4th or 5th edition.
Problem Solving Video
- Watch the recitation video on Problem Solving: Orthogonal Vectors and Subspaces
- Recitation video transcript (PDF)
Check Yourself
Problems and Solutions
Work the problems on your own and check your answers when you’re done.








