18.06SC | Fall 2011 | Undergraduate

Linear Algebra

Unit III: Positive Definite Matrices and Applications

« Previous | Next »

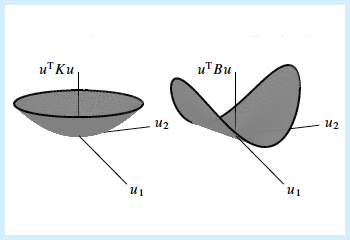
Positive definite and semidefinite: graphs of x’Ax.

In this unit we discuss matrices with special properties – symmetric, possibly complex, and positive definite. The central topic of this unit is converting matrices to nice form (diagonal or nearly-diagonal) through multiplication by other matrices. Generally, this process requires some knowledge of the eigenvectors and eigenvalues of the matrix.

Looking for something specific in this course? The Resource Index compiles links to most course resources in a single page.

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang

Video cameras record data in a poor format for broadcasting video. To transmit video efficiently, linear algebra is used to change the basis. But which basis is best for video compression is an important question that has not been fully answered!

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 7.2 in the 4th edition or Section 8.2 in the 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang

The Fourier matrices have complex valued entries and many nice properties. This session covers the basics of working with complex matrices and vectors, and concludes with a description of the fast Fourier transform.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 10.2 through 10.3 in the 4th edition or Section 9.2 and 9.3 in the 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

« Previous | Next »

Session Overview

This exam starts with a question about singular values. They all equal 1 when ATA = I. Question 2 in the exam uses eigenvalues and eigenvectors to compute powers of A: diagonalize first! 

Check Yourself

Exams and Solutions

« Previous | Next »

« Previous | Next »

Session Overview

Exam 3 covers the understanding of matrices through their eigenvalues. Elimination is history now, because it does NOT preserve eigenvalues. Notice the special types of matrices (like positive definite) and their factorizations.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Review Chapters 6 and 7, plus Sections 10.2 through 10.3 in the 4th edition or Review Chapters 6, 7, and 8 plus Sections 9.2 through 9.3 in the 5th edition.

Problem Solving Video

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang

We’d like to be able to “invert A” to solve Ax = b, but A may have only a left inverse or right inverse (or no inverse). This discussion of how and when matrices have inverses improves our understanding of the four fundamental subspaces and of many other key topics in the course.

Note: In the Fall of 1999, when the lecture videos were recorded, this lecture was given after exam 3. For the OCW Scholar version of the course we have moved it into the main body of material.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 7.3 in the 4th edition or Section 8.3 in the 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang

When we multiply a matrix by an input vector we get an output vector, often in a new space. We can ask what this “linear transformation” does to all the vectors in a space. In fact, matrices were originally invented for the study of linear transformations.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 7.1 in the 4th edition or Section 8.1 in the 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang In calculus, the second derivative decides whether a critical point of y(x) is a minimum. For functions of multiple variables, the test is whether a matrix of second derivatives is positive definite. In this session we learn several ways of testing for positive definiteness and also how the shape of the graph of ƒ(x) = xT Ax is determined by the entries of A.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 6.5 in the 4th or 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang

After a final discussion of positive definite matrices, we learn about “similar” matrices: B = M−1AM for some invertible matrix M. Square matrices can be grouped by similarity, and each group has a “nicest” representative in Jordan normal form. This form tells at a glance the eigenvalues and the number of eigenvectors.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 6.6 in the 4th edition or Section 6.2 in the 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang If A is symmetric and positive definite, there is an orthogonal matrix Q for which A = QΛQT . Here Λ is the matrix of eigenvalues. Singular Value Decomposition lets us write any matrix A as a product UΣVT where U and V are orthogonal and Σ is a diagonal matrix whose non-zero entries are square roots of the eigenvalues of ATA. The columns of U and V give bases for the four fundamental subspaces.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 6.7 in the 4th edition or Section 7.1 and 7.2 in the 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

« Previous | Next »

Session Overview

Figure excerpted from 'Introduction to Linear Algebra' by G.S. Strang

Special matrices have special eigenvalues and eigenvectors. Symmetric and positive definite matrices have extremely nice properties, and studying these matrices brings together everything we’ve learned about pivots, determinants and eigenvalues. In this session we also practice doing linear algebra with complex numbers and learn how the pivots give information about the eigenvalues of a symmetric matrix.

Session Activities

Lecture Video and Summary

Suggested Reading

  • Read Section 6.4 through 6.5 in the 4th or 5th edition.

Problem Solving Video

Check Yourself

Problems and Solutions

Work the problems on your own and check your answers when you’re done.

« Previous | Next »

Course Info

Departments
As Taught In
Fall 2011
Level
Undergraduate
Topics
Learning Resource Types
Lecture Videos
Exams with Solutions
Lecture Notes
Recitation Videos
Problem Sets with Solutions
Simulations
Course Introduction
Instructor Insights
Download Course
MIT Open Learning
Over 2,500 courses & materials
Freely sharing knowledge with learners and educators around the world. Learn more
© 2001–2024 Massachusetts Institute of Technology
Accessibility
Creative Commons License
Terms and Conditions
Proud member of:
© 2001–2024 Massachusetts Institute of Technology